Д. Рауп, С. Стэнли. «Основы Палеонтологии»

Фиг. 38. Распределение отношения ширины раковин к их длине у двух подвидов девонской брахиоподы Pholidostrophia [89]. A. Pholidostrophia gracilis nanus. Б. Pholidostrophia gracilis gracilis. Небольшое различие между средними величинами вполне может объясняться случайными ошибками при взятии выборок

Начиная исследование, необходимо решить, какое число морфологических признаков следует использовать. Многое зависит от того, намерены ли мы изучать различия или сходство между сообществами. Если мы хотим лишь показать, что два сообщества различаются между собой, то для этого достаточно и одной морфологической черты. На фиг. 37 показано распределение размеров особей двух подвидов брахиопод (измерялась максимальная ширина). Две диаграммы распределения перекрываются, но они явно различны. На фиг. 38 показаны распределения отношения ширины раковины к длине у тех же брахиопод. Не требуется сложной статистической обработки, чтобы понять, что по отношению ширины к длине оба сообщества не различаются сколько-нибудь существенно. Но из этого еще нельзя заключить, что оба сообщества одинаковы, — мы видим, что они различаются по ширине раковин (фиг. 37). Нередко неподготовленный исследователь, найдя близкое сходство в распределении каких-либо морфологических признаков у двух сообществ, делает вывод об идентичности этих сообществ, хотя между ними могут существовать важные различия, которые просто не отражены в использованных параметрах.

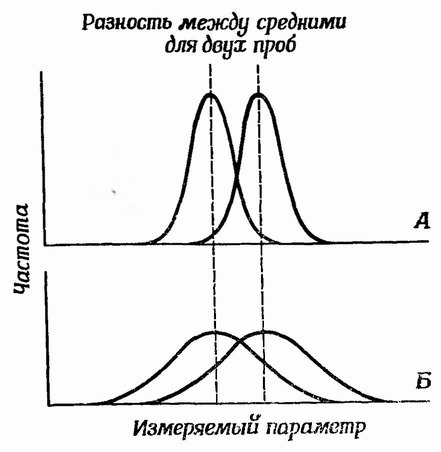
Фиг. 39. Пары гипотетических кривых распределения иллюстрируют важность изменчивости в определении смысла наблюдаемых различий между средними. В случае Б гораздо более вероятно, чем в случае А, что найденные различия объясняются случайностью

На фиг. 37 и 38 показаны крайние случаи, а между ними существует бесчисленное множество промежуточных. Для различения промежуточных случаев необходимы статистические методы. Прежде всего важно уметь определять, соответствует ли найденная изменчивость истинному положению вещей (т. е. можно ли ее интерпретировать с геологической или биологической точки зрения) или же она объясняется просто случайностью (в пробу случайно попали особи с такой изменчивостью). Для того чтобы выяснить, не объясняется ли обнаруженная при однофакторном анализе разница между средними простой случайностью, можно применить метод статистической проверки. Для этого нужно оценить не только разность между средними, но и диапазон изменчивости в каждом из двух сообществ. На фиг. 39 представлены две пары гипотетических распределений, иллюстрирующие важность оценки диапазона изменчивости. Здесь различия между средними одинаковы, но изменчивость значительно больше в выборке Б, чем в выборке А. Очевидно, в случае выборки Б более вероятно, что отмеченная разница между средними объясняется простой случайностью. Следовательно, вполне разумно будет включить выражение для изменчивости в оценку достоверности разности средних. Статистическая проверка не дает однозначного ответа типа «да» или «нет»; мы получаем лишь вероятность того, что найденная разность средних не случайна.

Всегда остается вопрос, какой должна быть эта вероятность, чтобы с уверенностью можно было сказать, что разность средних достоверна. Обычно за порог принимается вероятность 0,05. Иными словами, выборки можно считать различающимися, если мы на 95% уверены в том, что разность не объясняется случайностью. На первый взгляд это довольно жесткое требование. Но оно хорошо обосновано. Одно из главных соображений в пользу этой строгости — возможность ошибок даже при таком ограничении: если исследователь получил двадцать результатов и вероятность каждого из них 0,95, то не исключено, что один из результатов окажется неверным! Еще важнее, что если исследователь делает заключение, основанное на последовательности результатов, полученных ранее с таким же ограничением, то вероятность справедливости заключения оказывается значительно ниже 0,95. Если рассчитанная вероятность ошибки 0,05, то разность средних называют «статистически достоверной» при пятипроцентном пороге. Статистическая проверка сама по себе не дает никакой геологической или биологической информации, она лишь говорит нам, не могут ли найденные различия объясняться случайностью. Если полученная разность статистически достоверна, то остается проблема интерпретации происхождения обнаруженных различий.

Количественное изучение морфологических различий между ископаемыми сообществами обычно основывается на двухфакторном анализе. На фиг. 40 показано типичное двухфакторное сравнение данных по двум сообществам. Пользуясь математическим методом, через точки данных для каждой выборки провели прямую. Полученные прямые различаются по тому, в какой точке они пересекают ось ординат, и по наклону. Значит, два рассматриваемых подвида различаются по форме и по развитию формы в онтогенезе. Но достоверны ли эти различия статистически? Здесь необходимо применить критерии достоверности. Если окажется, что различия между прямыми достоверны, то можно будет заняться биологической или геологической интерпретацией этого факта.

Заметим, что на фиг. 40 приведены те же данные, что и на фиг. 37 и 38. Представленный на фиг. 40 график, показывающий связь двух параметров, объясняет, почему данные на фиг. 37 в отличие от фиг. 38 свидетельствуют о значительных различиях между исследуемыми выборками.

Для описания межпопуляционной изменчивости с учетом более чем двух факторов вместо формального многофакторного анализа используются также графические методы. Один из них, с применением символов, иллюстрируется на фиг. 41 Его основу составляет двухфакторный анализ. Измерялись некоторые признаки организмов, выбранных из двух популяций. Из них два параметра отложены по осям координат. Остальные признаки показаны на графике различными символами, значение которых объясняется рядом. Этот метод позволяет одновременно видеть различия по нескольким признакам; таким образом удается составить хотя и субъективное, но довольно верное представление о морфологических различиях между двумя сообществами. (На фиг. 41 использован непалеонтологический пример, поскольку диаграммы с символами пока редко применяются в палеонтологии.)

Фиг. 40. Двухфакторное распределение ширины и длины раковины у двух подвидов девонской брахиоподы Pholidostrophia [89]. Выборки те же. что на фиг. 37 и 38. Белые кружки — Р. gracilis gracilis; черные кружки — Р. gracilis nanus

Хотя символы позволяют охватить одновременно большее число признаков, чем при обычном двухфакторном или однофакторном анализе, все же остается проблема выбора признаков для сравнения. Если многофакторный анализ проводится с помощью ЭВМ, то число рассматриваемых признаков ограничивается только упорством исследователя и возможностями машины.

До сих пор мы как бы принимали, что измеряемые и сравниваемые признаки ископаемого независимы друг от друга в биологическом и геологическом отношениях. Однако известно, что многие морфологические признаки тесно зависят друг от друга. Связь эта может быть чисто механической. Например, любая структура, содержащая какие-либо внутренние структуры, всегда будет крупнее этих последних. Если построить график зависимости между размером одной структуры и размером другой, находящейся внутри нее, то станет ясно, что при увеличении первой будет увеличиваться и вторая.

Фиг. 41. Диаграмма с условными значками, использованная для анализа морфологических различий между двумя видами Aegilops, ближайшего родича пшеницы [241]

Более распространены функциональные связи между признаками. Например, створки раковины брахиоподы сходятся по линии комиссуры. Поскольку очертания створок имеют одинаковую форму и одинаковый размер, ни высокий коэффициент корреляции, получающийся при построении графика зависимости длины одной створки от длины другой, ни измерения другой створки не дадут новой информации по сравнению с измерениями первой створки. Размеры второй створки — избыточный признак.

<<   [1] ... [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] ...  [76]  >>